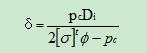内压圆筒计算
设计温度下的计算厚度按下式计算:
公式适用范围为pc ≤0.4∮[σ]或DO/Di≤1.5,公式中应力的推导是根据薄膜应力理论。采用第一强度理论,以圆筒平均直径为基准计算的环向应力,考虑了圆筒内壁上最大主应力与平均拉应力的差值进行了修正,并考虑了纵向焊缝(A类焊接接头)在强度方面相对于母材的削弱(图2.3)。
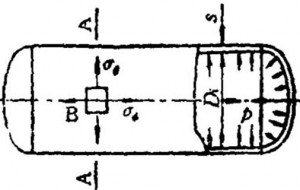
图2.3 内压圆筒计算示意
薄壁圆筒容器在工程中采用无力矩理论来进行应力计算,在内压P作用下,筒壁承受轴向应力 和切向应力(薄膜应力)作用。由于壳体壁厚较薄,且不考虑壳体与其他连接处的局部应力,忽略了弯曲应力,这种应力称为薄膜应力。
边缘应力
当圆筒形壳与圆球形壳或椭圆形壳相连的零部件受压后,各自产生的变形是不一致的,并相互产生约束,称为变形不连续。这时,除内压产生的膨胀外,还会产生附加的弯曲变形,与弯曲相对应,壳壁内将产生弯矩和剪力,称为边缘应力。对薄壁壳体来说,由此产生的弯曲应力有时比薄膜应力大得多,两连接件刚度相差越大,产生的应力也将越大。
在实际结构中,圆筒与平盖连接时的边缘应力最大,该应力由于只发生在两连接件的边界处,所以称为边缘效应力或称为不连续应力。由边缘力和边缘力矩引起的边缘应力具有局限性和自限性的特点。由于边缘应力具有局限性,设计中可以在结构上只作局部处理,例如改变连接处的结构、保证边缘焊接的质量、降低边缘区的残余应力以及避免边缘区附加的局部应力集中(如应避免在边缘区开孔)等。